前言
还记得上次推文结尾处，我说下次要写一写subgrid-scale physic processes，于是我查阅了一些资料，发现事情并不是那么简单，too naive ??。于是，我问李教授要了大气模式的书，从零开始学习。在此，基于自己一些浅显的理解，记录学习过程。
大气模式，看起来是一个非常复杂的东西，事实上也确实很复杂。然而，它所涉及到的物理知识，其实都是我们熟知的。大气模式的控制方程其实从是那个角度来阐述和模拟大气物理过程，分别是动量方程，连续方程，和热力学方程（Momentum equation, continuity equation, and thermodynamic equation），所涉及到的物理定律分别是牛顿第二定律，质量守恒和能量守恒，所以我说这些物理过程都是我们所熟知的。
今天这里先从连续方程入手，来看一看大气模式到底有何神奇之处，因本人学识尚浅，如有错误，请多包涵。
本文将从两个方面展开，首先介绍大气模式连续方程的基本知识，然后结合CMAQ，看看在具体的模式中是怎样考虑连续方程的。
大气模式中的连续方程
CMAQ中的连续方程
本部分介绍CMAQ中的连续方程，参考内容来自于EPA于1999年编写的Science Algorithms of the EPA Models-3 Community Multiscale Aiir Quality (CMAQ) Modeling System第五、六章，以下简称CMAQ科学算法。从名字可以看出来，CMAQ是一个区域型多尺度的大气模型，更确切的来说，它是一个基于三维欧拉网格方法的化学传输模型（Chemical Transport Model）。通过这部分内容，来欣赏一下CMAQ处理问题中模块化的思想。
另外，本文篇幅较长，公式较多，希望能够耐心看下去。观看过程中可能需要一些额外的背景知识，这里给出一些资源以作参考，希望能够有所帮助。
连续性方程（Continuity equations） 用于模拟变量的浓度或混合比随时间的变化，并考虑了变量的传输，外部源和汇。
假设烟羽中携带的气体的浓度为N = N（x[t],y[t],z[t],t）（mole.cm -3）。这里N是时间和空间的函数，将N对时间做全微分，可以得到：
这里的u，v，w分别是烟羽在x，y，z方向上的运动速度。
也就是常说的 物质导数（Material Derivative 。式中 叫做当地导数 ，式中 叫做随体导数。物质导数的物理意义表明，流体微团的物理量随时间的变化率，等于该物理量由当地时间变化所引起的变化率与由流体对流引起的变化率的和。
1.2 连续方程
当空气在封闭的空间中运动且没有任何化学或物理过程对其产生影响时，整个空间中总计的空气质量将不会发生改变，也就是质量守恒定律。连续方程本质上就是质量守恒。
在大气模式中，我们将研究区域划分成一个个网格（grid cell），对于每一个网格而言，质量的流入减去质量的流出，就等于最终网格内的质量减去初始时网格内的质量。
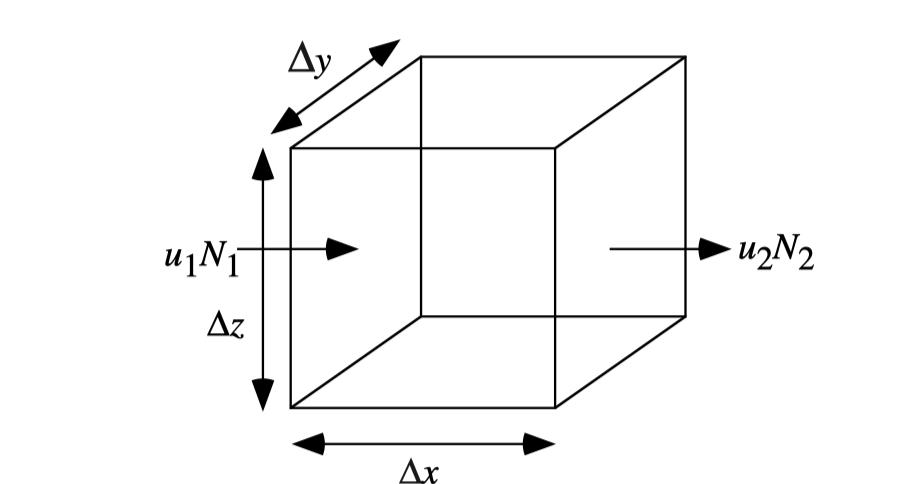图1.1 质量守恒例子
图1.1显示了尺寸为 的网格.进出该网格的前后标量速度分别为和。网格左右边界的气体浓度分别为和，所以进入和流出网格的气体质量流量分别为和.
根据给定的信息，在时间段t内进入，离开和累积在网格中的分子数分别为, 和
两边同除以时间和网格体积,得
当和，上式近似于
将上式扩展到笛卡尔坐标系中的三维空间，得到
方程（1.5）是连续方程的通量散度形式，之所以这么称呼是因为表示浓度的散度，散度实际上代表的就是物质的流入或流出。
由于
继而，对于浓度和气压，分别有如下式子
由于
这里表示速度散度，这些方程也是连续性方程的平流形式，因为包含平流项， 。这些方程式表明，运动微团中标量变量随时间的变化等于标量变量乘以速度的负局部空间梯度。
气体数浓度N（每立方厘米空气中的分子）与湿空气质量混合比 q（公斤/公斤湿空气），以及分子质量 m 有如下关系
其中，A是Avogadro’s number，将 带入中，得
根据和，给出关于单位为湿空气质量混合比 q 的气体连续性方程，
方程和表明空气是可压缩的（compressible），这意味着空气微团的总体积会随着时间而变化。海水被认为是不可压缩的，这意味着一小部分海水的总体积不会随时间变化。从而，
这是不可压缩流体的连续性方程。我们换一种表现形式，式相当于, 即速度散度为0时，表明流体不可压缩。当把带入中，得到
这表明不可压缩流体的密度沿流体的运动是恒定的。这里需要指出的是，对于流体的固定点，密度可能会改变。例如，将带入中，
这里可能会有读者对式和产生疑惑，注意这两式一个是全微分，一个是偏微分，所代表的物理含义不同，前者考察的流体流动过程中密度的变化，而后者只是在某一个固定的位置，流体的密度特性。总之，不可压缩流体（例如液态水）的密度可以在空间上变化，但是这种流体的总体积随时间是恒定的。在整个流体中密度在空间上变化的流体是不均匀的（inhomogeneous），例如海水。而如果对一个流体，式右侧恒为0，这时，流体被称为均匀的(homogeneous)。当然，空气是非均匀和可压缩的流体。
1.3 广义的连续方程
很明显，在之前的内容中，连续方程只考虑了流体本身的传输过程，而对流体分子扩散和外界的源与汇过程均为考虑。这里给出一个更加全面的连续方程，
式右式第二项为分子扩散项，D是分子扩散系数，分子扩散来自于分子间的相互碰撞。第三项则代表一些外界过程（化学反应，排放等）。现在我们将式展开，以供后续计算使用。
式子到这里似乎越来越复杂了。别着急，下面就是简化的过程了，我觉得简化的思想在数值模拟中十分重要，因为目前来看很多理论公式都不存在解析解或者无法算出解析解，那么怎么作出合理的物理假设和数学假设，在数值模拟过程中是必须要考量的一个问题。
思考一下，目前的大气模式都有时空分辨率的说法，也就是网格的大小和时间步长的大小。为什么我要提出这个呢？因为我们在做数值模拟的过程中，都是计算的某一时空分辨率下的平均值，如果我们还能够在细分，那我们的时空分辨率会更高。所以，其实我们可以将浓度的变化分成两个部分，即均值 扰动项，均值是主要的数值模拟过程，而扰动项呢？扰动项当然不可以直接去除，因为很多物理过程都是在次网格尺度下发生的，而针对这部分过程，在实际的过程中，我们采用参数化的思想来求解，这样问题就大大简化了。那我们来具体看一下，大气模式中是如何实现上述步骤的。其实上述过程叫做Reynolds averaging，使用雷诺平均处理湍流的模型称为雷诺平均模型（Reynolds-averaged models）。
在雷诺平均中，每个变量都被分解为平均项和扰动项，这种分解方式也被称为雷诺分解Reynolds decomposition。如下式，
这里N为实际（精确或者瞬时）浓度 ，为平均浓度，而为瞬时扰动浓度。在一个给定的网格和时间步长范围内，可以用积分的形式表示，
这里b代表时间步长，体积元素的含义与之前保持一致，这是针对单一网格和时间步长而言的，不同的网格和时间步长下平均浓度会发生改变。对于扰动项而言，雷诺认为其分布在均值的两侧，并且在时空范围内*所有扰动项的均值为0()*。
根据这个假设，我们对是那个速度分量做相同的分解，
依据上面的分解过程，我们将改写
由于，式中第一项可以简化为
由于和,第二项可以简化为
式中，代表次网格尺度涡流（subgrid-scale eddies），表示为运动湍流（kinematic turbulent ??ux），式中为湍流散度项（turbulent ??ux divergence term）。
我们对其他两个方向做同样的代换，最终得到
对大于分子尺度的运动，分子扩散项远小于湍流项，因此上式可以简化为
最后，用Nabla算子简写,得到气体连续方程（continuity equation for a gas），
类似的有，空气连续方程（continuity equation for air），
这里空气分子的外部源和汇项被忽略了，因为它们与其他项相比较小。然而在CMAQ中却保留了这一项，我们将在后面介绍为何要这么做。
到这里，连续方程的推倒基本段落。下面简单介绍一种参数化方案K-theory用于代替湍流项。
1.4 K-theory参数化方案
上文我们讲到，式中，代表次网格尺度涡流（subgrid-scale eddies），表示为运动湍流（kinematic turbulent ??ux），在大多数模式中，这一项都被用参数化（parameterization) 来代替。这里介绍一种常用的k-theory，也叫做梯度传输理论（gradient transport theory）。
在K-theory中，运动湍流由一个常数和一个波动变量平均值的梯度的乘积代替。这是啥意思，听起来挺绕的，在公式中将一目了然。我们以气体浓度为例，得到
其中，分别代表x,y,z方向上的涡流扩散系数（eddy diffusion coef??cients），下标b表示使用了能量的涡流扩散系数（涡流热扩散率）。涡流扩散系数代表所有小于网格的尺寸的涡流的平均扩散系数。涡流扩散系数也称为涡流转移，涡流交换，湍流转移和梯度转移系数。
涡流扩散系数是能量和动量的次网格规模输运的参数化。在垂直方向，这种运输是由机械剪切力（机械湍流）和/或浮力（热湍流） 引起的。当风在粗糙表面上流动时，水平风切变会产生涡流，涡流的大小会增加。浮力造成不稳定，导致剪切诱导的涡流变得越来越宽和越来越高。涡流中的垂直运动使地面空气向上流动，而空气向下流动。涡流也可以水平交换空气。
我们将式带入式中，得到
现在式中只有均值项，而均值项我们可以通过式积分式求解。为简单起见，压缩并去除了横线，以数浓度单位表示了单个气体的连续性方程（continuity equation for an individual gas in number concentration units），在笛卡尔坐标表示为
其中，
最后，我们将源汇项简单拆解，得到最终的气体连续方程（gas continuity equation）
其中，代表排放，代表干沉降，水洗，代表光化学反应过程，代表成核过程，代表冷凝/蒸发，代表沉积/升华，代表溶解/蒸发，代表异相反应。
2 CMAQ中的连续方程
在第一部分中，介绍了普遍适用的大气模式连续方程，而在具体的模式中，需要考量的更多，包括与气象模式产生的气象场的结合，同时我们还需要将笛卡尔坐标系转化为曲面坐标等等，这些都是我们在后续内容中需要学习的。
在CMAQ中，我们采用曲面坐标的方式来进行计算，曲面形式能够简化方程和计算过程。由于涉及到曲面方程，在CMAQ中，所有的控制方程将采用张量的形式表示，这在一定程度上造成理解障碍，事实上，我如今仍未看懂，CMAQ中关于笛卡尔系到曲面坐标系的转换过程，这部分内容在CMAQ科学算法第五章的附录A中，有兴趣的读者可参考自行推导。
2.1 一般曲面下的连续方程
在CMAQ中，选用密度和熵作为主要的热力学变量，建立控制方程。曲面坐标下的连续方程如下
其中，为密度，代表熵，为坐标变换的雅可比行列式，为风速的逆变基变量，代表方向，其中对应于笛卡尔系的x，y，z方向,，代表痕量气体浓度。代表源汇项。这三个式子看起来很复杂，实际上与笛卡尔系中的连续方程是一一对应的，拿式做说明，左边第一项就是1.1中的当地导数，第二项则是随体导数，源汇项则是相同的物理含义。
考虑到CMAQ作为一个多尺度的社区模型，用户根据实际需求，确定不同尺度下的研究区域，而往往不同尺度下的考虑的物理过程不尽相同，所以我们需要对上面三个原始公式加入空间变化特性，下面我们将对这些公式进行变换。将原始曲面坐标转化为,两者满足以下关系
其中，m为地图缩放因子，为地形高度，h为几何高度，为地上高度，将高度分解成这两项是因为地面高度不均匀。需要说明的是，在式的推导中，我们忽略了x，y方向上的一阶地图缩放系数。这个近似过程使得变换后的坐标垂直方向与水平方向呈准正交（quasi-orthogonality）形态（这句话没看懂??）。现在我们可以通过上式来计算协变量度量张量（covariant metric tensor），（这个推导过程还是需要张量基础，没看懂??）结果如下
则有
现在我们将上式带入到最初的连续方程。在此之前，我们先将连续方程拆分成水平和垂直两个方向，分别计算。代表水平方向，代表垂直方向，代表坐标变换的雅可比行列式。规定完这些后，我们将其带入原始连续方程，得到
2.2 CMAQ中气体连续方程
这一部分内容主要针对式。在推导之前，先来看一下CMAQ为了实现统一的多尺度运算，做了哪些假设。
假设1：污染物浓度足够低，以致它们的存在不会在任何可检测的范围内影响气象。因此，该物种守恒方程可以独立于Navier-Stokes方程和能量方程求解。 可能使该假设无效的条件是以下情况：化学反应产生的热量足以影响介质的温度，或者大气层中的污染物变得如此集中，以致吸收，反射和辐射散射会改变气流。假设2：各种物质在大气流中的速度和集中度是湍流量并且经历湍流扩散。 由于大多数痕量物质的湍流扩散远大于分子扩散，因此后者可以忽略不计。假设3：定义坐标变换规则的度量张量不是湍流变量。 这意味着我们根据雷诺平均数量来调用定义坐标。当使用时间相关的垂直坐标时，将在时间步长之间递增定义垂直网格。假设4：遍历假说适用于整体平均过程。这意味着可以将某个属性的整体平均值替换为该属性的时间平均值。假设5：在感兴趣的平均时间段内假设湍流是静止的（例如在大气应用中为30分钟到1小时）。假设6：源函数（即污染物的排放）对于所有实际目的都是确定性的，并且没有湍流成分。假设7：浓度波动对化学反应速率的影响可以忽略不计，即，示踪物种之间协方差效应的贡献可以忽略。假设8：由于大气的大规模运动相对于地球表面是准水平的，因此科学过程可以在水平和垂直方向上分开表示（在转换后的坐标中为准正交）。
依据雷诺分解，将瞬时浓度分解为均值项和湍流项。
其中，为物种质量混合比。根据假设5，湍流项的均值为0。变换得到
为不失一般性，我们将垂直方向的坐标改写
将上述公式带入到式中，得到
需要说明的是，基于假设3和假设6，坐标转化和源排放都不包含湍流过程，所以，。将式各项展开，根据章节1.4 K-theory的推导，我们知道均值项与湍流项的乘积为0，并且
改写式，得到
至此，我们得到了CMAQ中较为完整的气体连续方程，后续将通过K-theory进行参数化分解。
2.3 CMAQ中的K-theory
引入K-theory进行参数化。
式中,转化后坐标系的湍流扩散系数，它与笛卡尔坐标系中的湍流扩散系数满足以下关系
我们已经知道在笛卡尔坐标系中，是一个对角矩阵，而在曲面坐标系中，的形式将复杂一些，具体如下
这其中,为笛卡尔坐标系下的湍流扩散系数。为了保持计算网格一致，依据式,将中的(x,y,z)替换成,得到
将参数化矩阵带入式（2.9）中，有如下
和
将上两式带入到（2.9）中，并用对源项的明确描述来分离对角线和非对角线扩散项，可以在广义坐标系中获得主导的大气扩散方程，其中湍流项用涡流扩散理论表示：
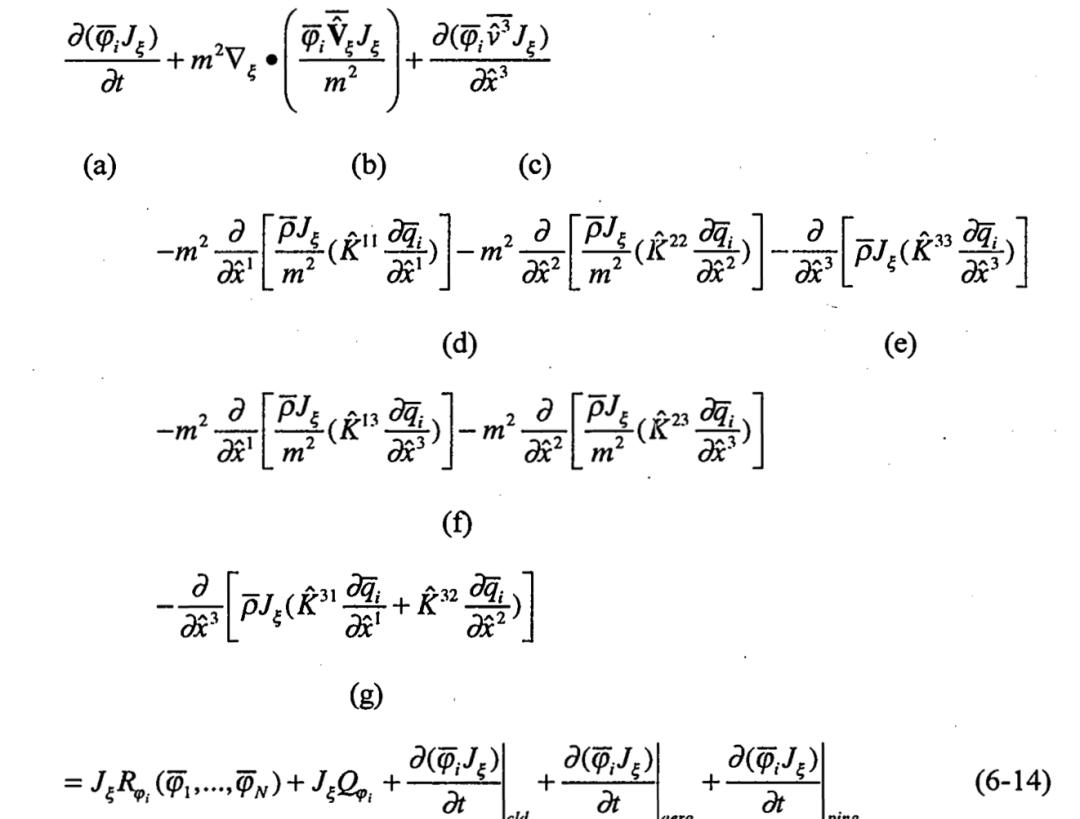公式（2.29）（下标很难对齐，这里直接截图了）
其中
(a) 污染物浓度的时间变化率(b) 水平平流(c) 垂直平流(d) 水平涡流扩散（对角项）(e) 垂直涡流扩散（对角项）(f) 非对角项的水平扩散(g) 非对角项的垂直扩散(h) 化学反应生成或损失(i) 排放(j) 云混合和液相化学反应生成或损失(k) 气溶胶过程(l) 网格烟羽过程
需要说明的是，干法沉积过程可以作为垂直扩散过程包含在模型层底部的通量边界条件。
为了简化方程使其看起来不那么复杂，下面介绍了一些记号的表示方法，
湍流项与笛卡尔直角对等项的转换关系
最后，就是用（2.31）代入（2.29），简化方程
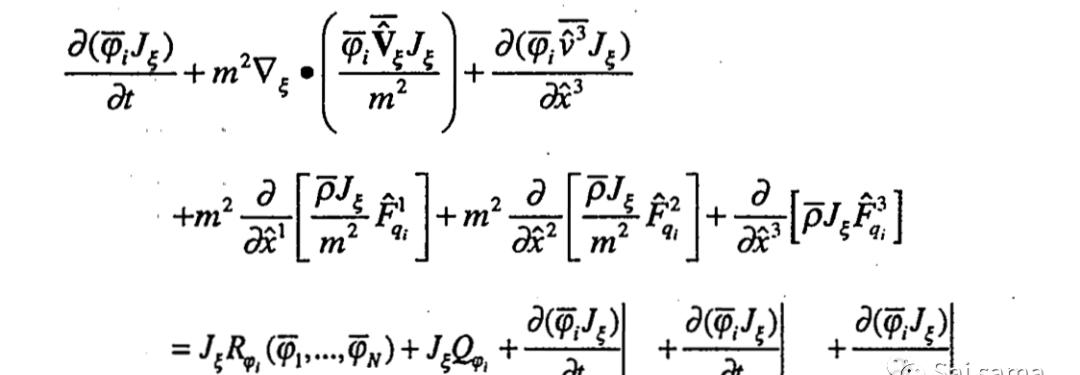式(2.32)
对于具有缓和地形的域，可以简化该控制方程，对于该域，可以忽略与垂直于垂直坐标的表面的水平梯度有关的所有项。这迫使曲线坐标系中的垂直扩散项与正交笛卡尔坐标系中的相同。然后可以用更简单的形式写出痕量物种守恒方程：
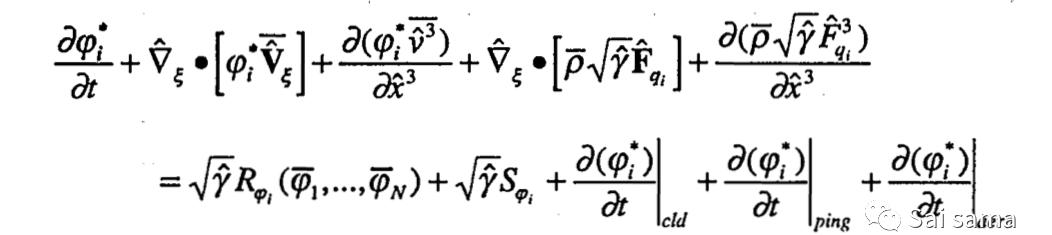式(2.33)
其中
,通过改写原公式，我们已经明确标识了与CMAQ中实施的科学过程模块直接相关。至此，推导结束。
总结
针对第一部分
根据质量守恒，建立浓度的连续方程。明白物质导数的意义，流体中物理量随时间的变化率不同于刚体运动，因为我们不是再将物体看作是一个质点，而是从拉格朗日或者欧拉角度来考虑物理的运动过程。明确物质导数由两部分组成，当地导数和随体导数，分别代表的是流体随时间的变化率和流体空间的变化率。根据雷诺分解，我们将流体的物理量（汝浓度）拆分成平均项和扰动项，并规定扰动项在平均值上下波动，在整个过程中扰动项之和为0.根据K-theory，将气体连续方程中的湍流项拆分出，进行参数化，简化模型计算。
针对第二部分
CMAQ中采用了曲面坐标，并且加入缩放因子，使得坐标系能够进行多尺度选择。CMAQ中同样采用K-theory对气体连续方程进行拆分，但CMAQ中的公式更为复杂，主要体现在两点，一是坐标变换带，二是CMAQ将水平与垂直方向完全拆开，原本的平流拆分成水平平流和垂直平流，原本的湍流项拆分成水平涡流扩散和垂直涡流扩散，将传输过程拆分的更细，这要做主要是基于模块化的思想以及简化运算，而本质上与第一部分没有区别。后记
就这样啊吧，累了??。张量那块看了很久，还是不清晰，有时间再看吧。下周真的要开始看托福了，不能在这死磕了??。
